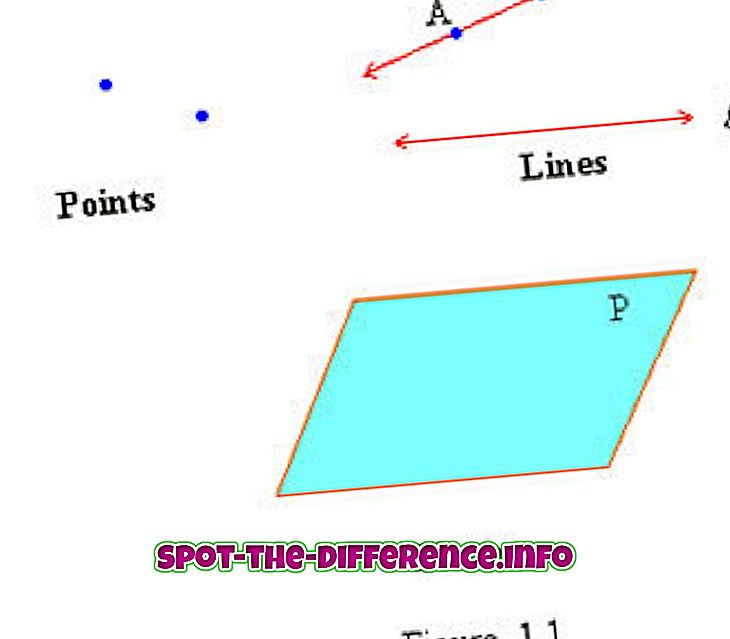
Galvenā atšķirība: punkts ir punkts, kas apzīmē vietu, kas ir atzīmēta uz bezgalīgas telpas vai plaknes virsmas. Līnija tiek uzskatīta par vienu dimensiju un tika ieviesta, lai attēlotu taisnus objektus bez platuma un dziļuma. Plakne ir divdimensiju plakana virsma, kas ir bezgalīgi liela ar nulles biezumu.
Punktu, līniju un plakni uzskata par nenoteiktiem ģeometrijas terminiem, jo tie nav oficiāli definēti. Kad mēs definējam terminu, tas parasti izmanto vienkāršākus vārdus, lai aprakstītu terminu. Tomēr punktu, līniju un plakni uzskata par jau vienkāršotiem noteikumiem. Visas pārējās ģeometriskās koncepcijas tiek veidotas uz punkta, līnijas un plaknes. Tomēr mēģināsim saprast šos trīs nenoteiktos terminus.
Punkts ir punkts, kas nenozīmē lietu, bet gan pozīciju. Punkts ir vieta, kas ir atzīmēta bezgalīgā telpā vai plaknē. Punkts var būt jebkura izmēra punkts, bet tam nav garuma, platuma vai biezuma. Tas ir tāpēc, ka tā ir vieta, nevis lieta.
Punkti tiek nosaukti, izmantojot lielo burtu, piemēram, A, B, C utt. Divdimensiju Eiklīda telpā, kas labāk pazīstama kā režģis vai grafiks ar x-asi un y-asi, punktu attēlo pasūtīts pāris (x, y). X apzīmē punkta horizontālo izvietojumu, bet y ir vertikālais izvietojums. Ir divi punkti: kolinārs un koplīnijas. Kolināru punktu kopums atrodas taisnā līnijā, savukārt koplīniju līniju kopums atrodas vienā plaknē.
Līnija tiek uzskatīta par vienu dimensiju un tika ieviesta, lai attēlotu taisnus objektus bez platuma un dziļuma. Līnijas definīcija mainās atkarībā no ģeometrijas veida. Eiklida ģeometrijā līnijai nav noteiktas definīcijas. Analītiskajā ģeometrijā līnija plaknē ir definēta kā punktu kopums, kuru koordinātas atbilst noteiktajam lineārajam vienādojumam. Saslimšanas ģeometrijā līnija var būt neatkarīgs objekts no punktiem, kas atrodas uz tā.
Līnija ir pieņemta kā viena dimensijas bezgalīgs punktu skaits, kas ir savienoti. Taisna līnija ir īsākais attālums starp diviem punktiem plaknē. Līnijas katra ir atzīmētas ar divām bultiņām, lai norādītu, ka tā nekad nebeidzas. Līnijas tiek nosauktas divos veidos: ar diviem punktiem līnijā vai ar vienu mazo burtu kursoru. Jebkurus divus punktus, kas atzīmēti uz līnijas, var izmantot, lai atsauktos uz līniju. Piemēram: Līnija ar punktiem H, I uz tā būs apzīmēta ar līniju HI, un tā tiks novietota virs tā, lai norādītu, ka tā ir līnija.
Plakne ir divdimensiju plakana virsma, kas ir bezgalīgi liela ar nulles biezumu. Plakne tiek uzskatīta par divdimensiju punktu (nulles izmēri), līniju (vienu dimensiju) un cietu (trīsdimensiju). Apsverot definīciju Eiklīda telpā, plakne attiecas uz visu telpu. Iedomājieties metāla loksni, kurai nav biezuma, tomēr tas notiek uz visiem laikiem. Tas tiek uzskatīts par plakni.
Wikipedia norāda, ka „daudzi pamatuzdevumi matemātikā, ģeometrijā, trigonometrijā, grafu teorijā un grafikā tiek veikti divdimensiju telpā vai, citiem vārdiem sakot, plaknē.” Lai gan plaknes ir bezgalīgas, zīmēšanas dēļ, tām ir nepieciešama malām. Šīs lidmašīnas uzzīmē ar diviem paralēliem pāriem un izskatās kā slīpais taisnstūris. Plaknei ir divi izmēri: garums un platums. Bet tā kā plakne ir bezgalīga, garumu un platumu nevar izmērīt.
Lidmašīnas nosaka trīs punkti. Ir divu veidu lidmašīnas: paralēlas plaknes un krustojošās plaknes. Paralēlās lidmašīnas ir divas vai vairākas lidmašīnas, kas bezgalīgi šķērso viena otru. Iedomājieties agrāko metāla loksni, tagad pievienojiet vēl vienu metāla loksni, kas atrodas uz tā, un turpinās arī uz visiem laikiem. Šie divi veidotu divas paralēlas plaknes, kas nekad nepārkāps. Tomēr interesantas lidmašīnas ir tieši tas. Tās ir divas plaknes, kas šķērso viena otru. Lidmašīnas parasti tiek nosauktas ar vienu lielo burtu, kas rakstīts kursīvā (plakne P).
Ģeometrijā punkts, līnija un plakne tiek apvienoti postulāta veidā. Šis postulāts ir trīs pieņēmumu (aksiomu) kopums, ko var izmantot kā daļu no eiklīda ģeometrijas pamatiem trīs vai vairāk dimensijās. Trīs pieņēmumi ietver: unikālu līniju pieņēmumu, numura rindas pieņēmumu un dimensijas pieņēmumu. Unikālā līnija pieņēmums liecina, ka ir tieši viena līnija, kas iet caur diviem atšķirīgiem punktiem. Numuru rindas pieņēmums norāda, ka katra līnija ir punktu kopums, ko var ievietot viena pret vienu sarakstē ar reāliem skaitļiem. Jebkurš punkts var atbilst 0 (nulle) un jebkurš cits punkts var atbilst 1 (viens). Visbeidzot, dimensijas pieņēmumi norāda, ka plaknei ir līnija, plaknē ir vismaz viens punkts, kas nav uz līnijas. Ņemot vērā plakni telpā, ir vismaz viens punkts telpā, kas nav plaknē.