Galvenā atšķirība: matemātikā vienādojumu izmanto, lai apzīmētu divu izteiksmju vienlīdzību. No otras puses, funkcija ir daudz sarežģītāka nekā vienādojums. Funkcija tiek izmantota, lai apzīmētu attiecību starp ievades kopumu un atbilstošu izeju kopumu.

Vienādojums un funkcija ir divi no algebras pamatiem, matemātikas priekšmets. Abi var būt diezgan sarežģīti, tomēr to pamatveidā tie var tikt sajaukti viens ar otru. Galvenā atšķirība starp vienādojumu un funkciju ir fakts, ka vienādojums parasti attiecas uz vienu ieeju, bet funkcijai var būt daudz ievades.

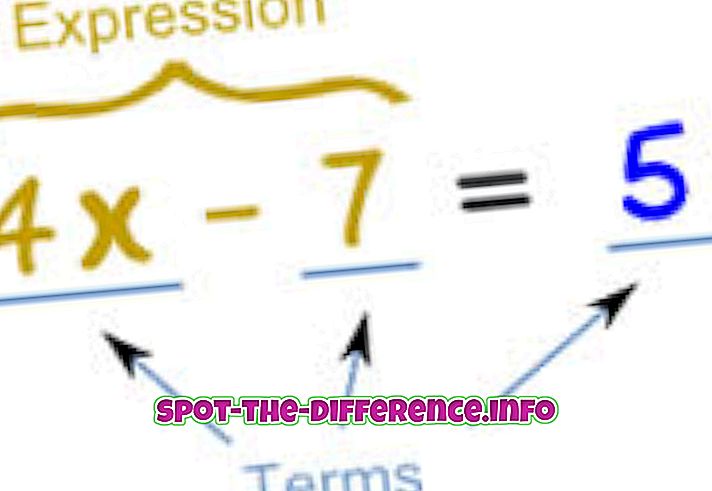
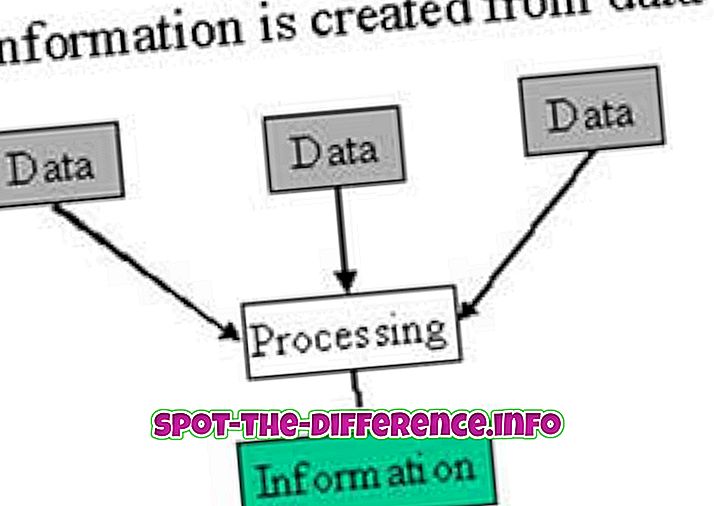
Matemātikā vienādojums tiek lietots, lai apzīmētu divu izteiksmju vienlīdzību. Būtībā vienādojums ir rakstīts kā izteiksme, kas atbilst citai izteiksmei. Piemēram: x + 2 = 5. Tas nozīmē, ka neatkarīgi no tā, kas ir x, ja pievienosiet to 2, tas būs vienāds ar 5. Tādējādi mēs varam atrisināt vienādojumu x, kas ir 3, kā 3 + 2 = 5.

Vienādojumi var būt sarežģītāki par to un var ietvert vairāk nekā vienu mainīgo, piemēram, x, y, z utt. Vienā vienādojumā. Piemēram: 3x + 2y - z = 4. Tomēr katrs alfabēts atbilst vienam skaitlim. Šajā gadījumā x = 1, y = 2 un z = 3.

Līdz ar to

3x + 2y - z = 4 kļūst

3 (1) + 2 (2) - 3 = 4, kas ir

3 + 4 - 3 = 4 būtībā

4 = 4

No otras puses, funkcija ir daudz sarežģītāka nekā vienādojums. Funkcija tiek izmantota, lai apzīmētu attiecību starp ievades kopumu un atbilstošu izeju kopumu. Būtībā ieejai vajadzētu dot vienu izeju. Funkcija ir saikne starp diviem mainīgajiem. Piemēram: f (x) = x + 2. Saskaņā ar šo funkciju, neatkarīgi no tā, kāda ir ieeja, tā dos jums vienu izeju, kas būs ieeja plus 2. Atrisinīsim šo funkciju:

Ievade	Funkcija	Izeja
x	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Un tā tālāk…

Funkcijām ir dažādi pielietojumi matemātikā, fizikā, datorzinātnēs utt. Tie var būt no vienkāršas funkcijas, kā norādīts iepriekš, līdz sarežģītām formulām vai algoritmiem. Funkciju var uzskatīt par mašīnu, kas dod izeju ieejai, un šī izeja ir kaut kādā veidā saistīta ar ievadi.

Funkcijai vienmēr ir trīs daļas: ievade, attiecības un izeja. Klasisks veids, kā rakstīt funkciju, ir ar "f (x) = ...", kur x apzīmē ievadi un f (x) apzīmē izeju.

Kā minēts iepriekš, galvenā atšķirība starp vienādojumu un funkciju ir tāda, ka vienādojumam parasti ir tikai viens ieeja, kas novedīs pie tā, ka izteiksmes ir vienādas. Tā kā funkcijai ir dažādi ievadi, no kuriem katrs dos produkciju.